Mechanical engineers analyze the dynamic behaviour of machine tools in frequency domain. Resonance or antiresonance frequency are familiar concepts used to describe the structural dynamic response of a machine tool. What about using these concepts in thermo-mechanical analyses? Does a machine tool show a thermal resonance frequency? If you would like to know more about these topics, keep on reading this blog post.
Understanding the thermo-mechanical FRF
In order to visualize the effect of frequency in the thermo-mechanical behavior, we are going to carry out a simple experiment. Back in the 60s, Brewer [1] published for the first time the concept of thermal resonance frequency for metrology of workpieces. In this blog, we are going to revisit his work, shown in Figure 1, using current visualization techniques.
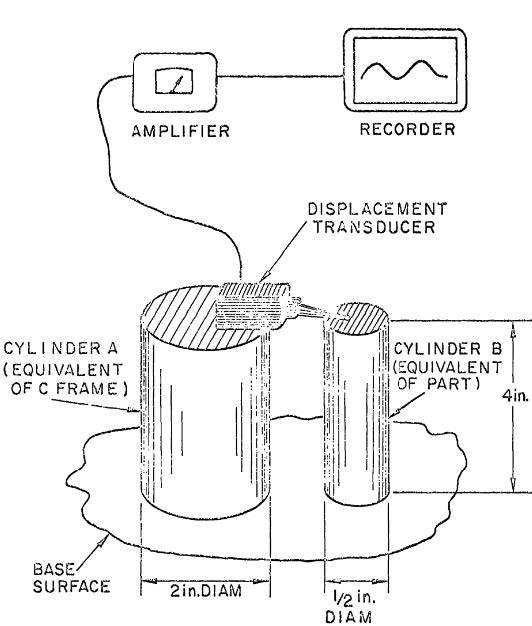
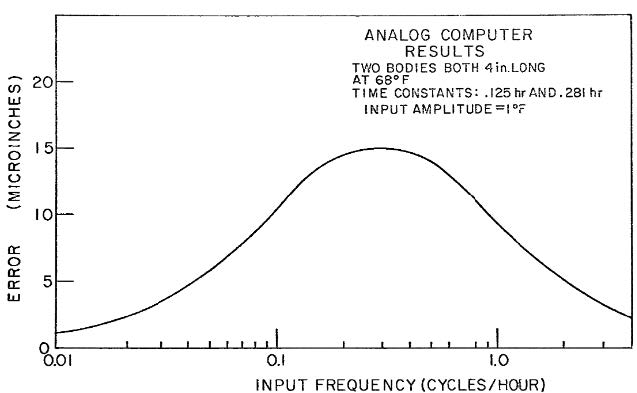
Figure 1. Thermal resonance concept, adapted from Brewer et al. [1]
We have two workpieces made of the same material, steel, and same nominal length. The only difference between the two parts is their diameters, 50 and 10 mm respectively. We perform the measurements in a temperature controlled chamber, where the temperature oscillates harmonically. The amplitude of the oscillation is 1K. While we modify the temperature of the room, a displacement transducer captures the difference in length between the two parts.
a. Low frequency
b. High frequency
c. 8 h periodicity
Figure 2. Animation of the thermo-mechanical response of two workpieces to fluctuations of the environmental temperature at different frequencies
Let’s assume a very slow oscillation of the air temperature, with very few cycles per hour. The slow changes of the air temperature provide enough time to both of the workpieces to elongate simultaneously, as shown in the Figure 2a. Therefore, the difference in length of the two parts is negligible and the displacement transducer measures a zero value.
Another interesting case is looking at what happens when the air temperature oscillates at a high frequency, that is, with many cycles per hour. In this case, the fast variation of the air temperature does not allow enough time for the parts to react. The temperature of the workpieces remains constant, leading to no elongation of the parts as illustrated in Figure 2b. Therefore, the measurement of the displacement transducer is zero.
We have described the output of the displacement transducer when the air temperature oscillates at either low or high frequency. But what about intermediate frequencies? For this frequency range, our experiment becomes more interesting. On one hand, the cylinder with the smaller diameter has a low thermal capacity. Therefore, this part has enough time to react to the variations of the air temperature. On the other hand, the air temperature oscillates too fast to allow the larger cylinder to fully heat up and cool down. Therefore, the temperature changes and the resulting elongation are smaller for the workpiece with the larger diameter. This difference between the elongation of the parts leads to a non-zero measurement of the displacement transducer, as shown in Figure 2c.
If we do this analysis for every single frequency, we obtain the frequency response function (FRF) of the thermo-mechanical behavior. In Figure 3, we can observe that the amplitude of the measurement reaches a maximum at a certain frequency. In the literature, this frequency is called thermal resonance frequency.
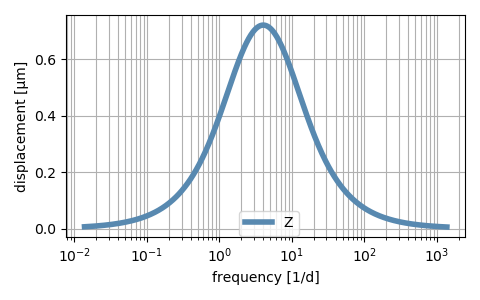
Figure 3. Thermo-mechanical FRF of the two workpieces. The input is the environmental temperature. The output is difference between the height of the workpieces (Z-direction)
This example shows conceptually the effect of frequency in the thermo-mechanical response of two parts. These ideas can be extended to a whole machine tool. The difference between the thermal masses of the components of the machine tool might lead to a maximum value of the FRF, resulting in thermal displacements between the tool center point (TCP) and the workpiece.
Thermo-mechanical FRF in MORe
In MORe, we designed a dedicated analysis to evaluate the thermo-mechanical FRF, keeping the workflow as simple as possible. The user needs to define the thermal loads, such as convection or heat fluxes, which are used as inputs to the FRF. After defining the frequency range where the FRF is going to be evaluated, you are ready to press the start simulation button.
In the postprocessor, the viewer allows to visualize the FRF for different inputs and output combinations. Furthermore, you can animate the temperature field as well as the thermo-mechanical deformation at any desired frequency.
Thermal resonance frequency of the RMT
After reviewing the concept of thermo-mechanical FRF and showing its implementation in MORe, we are ready to perform a thermo-mechanical FRF analysis in a machine tool model. This blog post uses the thermo-mechanical model presented in our previous blog post Welcome to the world of thermo-mechanical simulations: environmental temperature effects. The machine tool used for this post is the RMT, a 3-axis machine tool with linear direct drives.
The machine tool is exposed to the environmental temperature. The oscillation of the air temperature is going to be the input of the FRF. Furthermore, the spindle and the linear drives are cooled. For this analysis, we assume that the cooling temperature remains constant, that is, the cooling temperature is not an input of the FRF. As the output, we select the TCP displacements relative to the table in Z-direction. We evaluate the FRF up to a frequency corresponding to a periodicity of 1 min.
Figure 4 shows the FRF of the RMT for the described input and output combination in the selected frequency range. We depict the frequency in cycles/day, in order to visualize the different characteristic periodicities. On one hand, the FRF shows that the themo-mechanical displacement in Z-direction is 2.8 μm/K, at low frequencies. On the other hand, the TCP displacements are negligibly small at high frequencies. In between, there is a maximum value of 5 μm/K, centered around the 8 h periodicity.
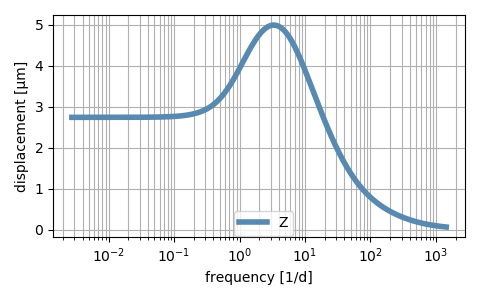
Figure 4. Thermo-mechanical FRF of the RMT. The input is the
environmental temperature. The output is relative displacement between TCP and workpiece in vertical direction (Z-direction)
In order to understand the FRF, we can visualize the temperature field and the associated structural deformation for any of the frequencies. Let’s start with a low frequency. This frequency represents the steady state response, or in other words the static gain of the system. Figure 5 shows that the whole temperature structure follows almost homogeneously the oscillation of ±1 K of the environmental temperature.
Figure 5. Thermo-mechanical response of the RMT to environmental temperature at low frequencies (steady state)
The cooling remains active and at a constant temperature for this simulation. Therefore, there are temperature gradients inside the structure visible around the spindle. The difference in the dimensions of the different structural parts combined with the effect of the structural cooling leads to a thermo-mechanical displacement at the TCP of 2.8 μm for a fluctuation of ±1 K at low frequencies.
Figure 6. Thermo-mechanical response of the RMT to environmental temperature at high frequencies
The response of the machine tool to fluctuations of air temperature at high frequencies is also interesting. Figure 6 shows that only the structural parts with a small thermal capacity react to the input. However, the speed of the oscillation of the input does not allow enough time for the parts to exchange heat with the environmental air through convection. Therefore, the amplitude of the FRF at high frequencies is close to zero.
Figure 7. Thermo-mechanical response of the RMT to environmental temperature with 8h periodicity (thermal resonance frequency)
Finally, we can visualize the deformation of the structure for a periodicity of the air temperature of 8 h. This period corresponds to the maximum value of the FRF. In Figure 7, we can see that the oscillation of the temperature of the structural parts with a large thermal mass is smaller than those parts with smaller mass. This is visible comparing the deformation of the bed and the spindle. The difference between the responses results in an increase of the thermo-mechanical displacements at this frequency, leading to a thermal resonance frequency.
During the design of the machine tool, the development engineer needs to avoid that the maximum values of the FRF appear at frequencies which might be often excited during the use of the machine tool. In order to optimize the thermal design, the engineer can modify the structural components, introduce cooling in specific areas, or isolate the structure from the environment.
Take-home message
FRF analyses visualize how the temperature and thermo-mechanical displacements of the machine tool react to a thermal load at any frequency. It allows you to identify if your machine tool concept has a thermal resonance frequency. While conceptually more challenging than time-domain analyses, the thermo-mechanical FRF is a powerful tool to understand your design.
Give it a try in MORe and open up a world of improvement potential to your machine tool design.
References
[1] Brewer W, Bryan J B, McClure E, Pearson J (1965) Thermal effects in dimensional metrology. In Mechanical Engineering, Band 87, 70. ASME-AMER SOC Mechanical Eng.

